Parallel biquad filter with CUDA
This is a direct follow-up to this post which in turn was a follow-up to this post. It re-iterates and explains some of the points made in these posts, and expands on them.
The problem: Biquad filter implementations might look like this (taken from libopus,
minus the fixed-to-float overhead, replacing the custom types with generic ones, and
removing the stride parameter):
static void silk_biquad_float(
const float *in, /* I: Input signal */
const float *B, /* I: MA coefficients [3] */
const float *A, /* I: AR coefficients [2] */
float *S, /* I/O: State vector [2] */
float *out, /* O: Output signal */
const int len /* I: Signal length */
)
{
/* DIRECT FORM II TRANSPOSED (uses 2 element state vector) */
int k;
float vout;
float inval;
for( k = 0; k < len; k++ ) {
inval = in[ k ];
vout = S[ 0 ] + B[0]*inval;
S[ 0 ] = S[1] - vout*A[0] + B[1]*inval;
S[ 1 ] = - vout*A[1] + B[2]*inval;
out[ k ] = vout;
}
}The problem is the S state vector. It gets updated with each iteration (for each sample)
and is also used to calculate the output value in each iteration. This makes it apparently
impossible to run the filter in parallel.
“Direct form 2 transposed” refers to one of the variations of the biquad filter and is explained on Wikipedia. A more generic and more compressed version of the filter, which doesn’t use a state vector, could look like this:
out[k] = B[0] * inp[k] + B[1] * inp[k - 1] + B[2] * inp[k - 2] - A[0] * out[k - 1] - A[1] * out[k - 2]Again the problem is that each output depends on two previously calculated outputs, making it apparently impossible to run this in parallel.
What can be run in parallel?
There are a number of existing algorithms that have parallel implementations. One such algorithm is the prefix sum, or sometimes called a scan. A prefix sum does something like this:
out[0] = inp[0];
out[1] = inp[0] + inp[1];
out[2] = inp[0] + inp[1] + inp[2];
...A scan is a more generic version of this, which uses an operator other than addition. It can be done with multiplication, or more generically any binary operator.
out[0] = op(inp[0], ID);
out[1] = op(inp[0], op(inp[1], ID));
out[2] = op(inp[0], op(inp[1], op(inp[2], ID)));
...Here ID refers to the identity element of the operator, which for addition is 0
and for multiplication is 1. This can be executed in parallel as long as the operator is
associative. (It’s not a requirement for the operator to be commutative.)
Complex binary operators
Consider the following generic multiply-and-add function:
F(x) = a * x + b
Here a and b are constants. Consider two of these functions with different specific constants:
F1(x) = a1 * x + b1
F2(x) = a2 * x + b2
These functions can both be represented by the generic F(x) version if the specific constants
(a1,b1) and (a2,b2) are supplied.
These can be composed as such:
F12(x) = F1(F2(x)) = a1 * (a2 * x + b2) + b1
F12(x) = a1 * a2 * x + a1 * b2 + b1
F12(x) = (a1 * a2) * x + (a1 * b2 + b1)
In other words, F12(x) is again in the form of F(x) with (a,b) now being (a1 * a2, a1 * b2 + b1).
This means that we can create a binary operator “compose” that takes two
functions of type F(x) (represented as (a,b)) as input and returns a new
function, also of type F(x), as output. This operator happens to satisfy the
requirement of being associative (but not commutative) and can therefore be used
in a parallel scan.
F12 = op(F1,F2)
The identity element for this operator would be the (a,b) representation for
a function which satisfies this condition:
Fx = op(Fx,ID)
Note that this also works if a, b, and x are matrices, which will become important later.
But how does this help?
State-space
The biquad filter can be represented as a transfer function, and transfer functions can be converted to state-space representation. In state-space representation, filter output is derived from the input as such:
state[k + 1] = p * state[k] + q * inp[k]
out[k] = r * state[k] + t * inp[k]
Here, p, q, r, and t are derived from the filter coefficients (B[3]
and A[2] for biquad – traditionally these values are given as A, B,
C, and D, but I changed them to avoid confusion with other a and b
values). At first glance this still doesn’t help because each new state is
still calculated based on the previous state. But at second glance the
derivation of each new state is exactly our F(x) function from above!
Therefore, still with each F(x) function represented by its (a,b) constants, we can
build a list of functions, one for each input, that returns the new state for that input.
The function corresponding to the first output would be the identity element, as
there is nothing to be done for state[0] (see below for an explanation):
F_state[0] = ID
The function belonging to the second output, or state[1], is:
state[1] = p * state[0] + q * inp[0]
Using our F(x) function, using state[0] as input x, we would have:
F_state[1](x) = p * x + q * inp[0]
In our (a,b) representation this therefore becomes:
F_state[1] = (p, q * inp[0])
For the third function, state[2], belonging to the third output, using the same approach we then have:
state[2] = p * state[1] + q * inp[1]
F_state[2](x) = p * x + q * inp[1]
F_state[2] = (p, q * inp[2])
Spelling this out, the resulting states now can be derived by:
state[0] = op(F_state[0], ID)
state[1] = op(F_state[0], op(F_state[1], ID))
state[2] = op(F_state[0], op(F_state[1], op(F_state[2], ID)))
Which is a scan and can therefore be done in parallel thanks to op() being associative.
Once all states have been calculated in this way, producing the output is then straight-forward and can also be done in parallel (see below).
Determining state-space values
If the B[3] and A[2] coefficients are known ahead of time and hard-coded, the p, q, r, and t
values can be calculated using Octave’s convenient tf2ss function:
octave:1> pkg load signal
octave:2> [p,q,r,t] = tf2ss([0.2 -0.3 0.4], [1 -0.6 0.7])
p =
1.1102e-16 7.0000e-01
-1.0000e+00 6.0000e-01
q =
0.2600
0.1800
r =
0 -1
t = 0.2000
octave:3>
(Why the extra 1 in the denominator? Because our version of the biquad filter
is normalised and a0 in the transfer function is therefore 1).
To do this at runtime, the values can be derived as such (taken from this paper which uses
the traditional A, B, C, and D for the state-space values, u for the input, y for the output,
and q for the state):
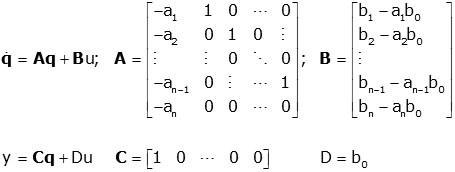
As these are matrices, the state for each output sample therefore will also be a matrix. Multiplications mentioned above therefore must be done as dot products, and additions as matrix additions respectively.
Output
Since we represent each state as a function with (a,b) constants that can be
composed with other such functions, and not directly as a state
itself, we must consider what each state should look like.
As per above, in each state function, a initially equals p, which is a 2×2 matrix, and b
initially equals q scaled by an input scalar, which is a 1×2 matrix. The binary
operator op() returns the new a as a1 * a2, which is still a 2×2 matrix, and the
new b as a1 * b2 + b1, which is still a 1×2 matrix.
As per state-space representation, output is then generated as such:
out[k] = r * state[k] + t * inp[k]
This is almost straight-forward: The output must be a single scalar value and the input is
also a single scalar value. As per the conversion formula above, our t always equals
B[0] and is therefore also a scalar. r on the other hand is not: it’s a 2×1 matrix. It
therefore requires a 1×2 matrix to be reduced to a scalar so that it can be used to create
a scalar value.
With the generic F(x) formula being F(x) = a * x + b and a being a 2×2 matrix and
b being a 1×2 matrix, the input x must therefore also be a 1×2 matrix so that a 1×2 matrix
can be returned. The initial state of the filter is zero (the first state calculated is state[1]
and therefore state[0] is zero), therefore the value for x to be used in all functions is the
[0;0] matrix. This reduces a * x to [0;0], leaving b as the only return value. To create
the output, this is then multiplied by r, which is always [1 0] if the
conversion formula above was used (Octave’s tf2ss can give
different results). Therefore the only value from each state relevant to produce the output
is b[0]. (For tf2ss output from Octave, this would be b[1] or -b[1].)
The identity element for (a,b) representing an F(x) style function is therefore
the 2×2 identity matrix for a and the 1×2 zero matrix for b (meaning ([1 0; 0 1], [0; 0])) which
also satisfies the requirement for a zero state[0] as b is all zeroes.
Implementation
A full implementation of this in CUDA is below, still vaguely based on the original code from libopus. This code is designed only for a single warp (32 threads) due to the use of warp-level shuffle intrinsics to perform the scan. Expanding this to larger block sizes using shared memory should be trivial. It can be expanded to an entire grid with a more sophisticated algorithm to perform the scan.
A more complete example with sample data is available here. There’s lots of room for additional optimisations.
__device__ static void silk_biquad_float_para(
const float *in, /* I: Input signal */
const float *B, /* I: MA coefficients [3] */
const float *A, /* I: AR coefficients [2] */
float *S, /* I/O: State vector [6] */
float *out, /* O: Output signal */
int len /* I: Signal length */
)
{
assert(blockDim.x == warpSize);
float Bx = B[1] - A[0] * B[0];
float By = B[2] - A[1] * B[0];
// one block at a time
while (len > 0) {
// thread 0 gets the initial saved state. everyone else fills the new state
float a00, a10, a01, a11, b0, b1;
if (threadIdx.x == 0) {
a00 = 1. + S[0]; // offset by 1 to allow for zero start
a10 = S[1];
a01 = S[2];
a11 = 1. + S[3]; // offset by 1 to allow for zero start
b0 = S[4];
b1 = S[5];
}
else if (threadIdx.x <= len) {
a00 = -A[0];
a10 = 1;
a01 = -A[1];
a11 = 0;
b0 = Bx * in[threadIdx.x - 1];
b1 = By * in[threadIdx.x - 1];
}
else {
// identity
a00 = 1;
a10 = 0;
a01 = 0;
a11 = 1;
b0 = 0;
b1 = 0;
}
for (int i = 1; i < warpSize; i *= 2) {
float a00_lower = __shfl_up_sync(FULL_MASK, a00, i);
float a10_lower = __shfl_up_sync(FULL_MASK, a10, i);
float a01_lower = __shfl_up_sync(FULL_MASK, a01, i);
float a11_lower = __shfl_up_sync(FULL_MASK, a11, i);
float b0_lower = __shfl_up_sync(FULL_MASK, b0, i);
float b1_lower = __shfl_up_sync(FULL_MASK, b1, i);
if (threadIdx.x >= i) {
// (a,b) = (a1 * a2, a2 * b1 + b2)
// dot products:
// a1 * a2 = [q w; e r] * [t y; u i] = q * t + w * u q * y + w * i; e * t + r * u e * y + r * i
// a2 * b1 = [q w; e r] * [t; y] = q * t + w * y; e * t + r * y
float tmp;
tmp = a00 * b0_lower + a10 * b1_lower + b0;
b1 = a01 * b0_lower + a11 * b1_lower + b1;
b0 = tmp;
tmp = a00_lower * a00 + a10_lower * a01;
a01 = a01_lower * a00 + a11_lower * a01;
a00 = tmp;
tmp = a00_lower * a10 + a10_lower * a11;
a11 = a01_lower * a10 + a11_lower * a11;
a10 = tmp;
}
}
// output
if (threadIdx.x < len)
out[threadIdx.x] = b0 + B[0] * in[threadIdx.x];
// advance block
len -= blockDim.x - 1;
in += blockDim.x - 1;
out += blockDim.x - 1;
// save state
if (threadIdx.x == blockDim.x - 1) {
S[0] = a00 - 1.; // offset by 1
S[1] = a10;
S[2] = a01;
S[3] = a11 - 1.; // offset by 1
S[4] = b0;
S[5] = b1;
}
__syncthreads();
}
}